Math Blog

Understanding Perpendicular Bisectors: Definition and Applications

Perpendicular bisectors are a fundamental concept in geometry that is used to describe lines that are perpendicular to each other and intersect at the midpoint of a given line segment. In this article, we will provide a definition of perpendicular bisectors and explore their applications in various contexts.

Definition of Perpendicular Bisectors

A perpendicular bisector is a line or segment that is perpendicular to a given line segment and intersects it at its midpoint. In simpler terms, it is a line that splits a line segment into two equal parts and is perpendicular to it.

For example, consider a line segment AB. The perpendicular bisector of AB would be the line that passes through the midpoint of AB and is perpendicular to AB. This line would divide AB into two equal parts, making it a perpendicular bisector.

Applications of Perpendicular Bisectors

Perpendicular bisectors have various applications in geometry and other fields, some of which are highlighted below:

Construction of Triangles

Perpendicular bisectors can be used to construct triangles. To do this, we draw the perpendicular bisectors of two sides of a triangle, which will intersect at a point called the circumcenter. The circumcenter is equidistant from the three vertices of the triangle and is the center of the circle that passes through the three vertices of the triangle.

Navigation Systems

Perpendicular bisectors are used in navigation systems to determine the location of an object. For example, consider an airplane traveling at a constant speed. Its location can be determined by measuring the distances from the airplane to three different radio beacons on the ground. The lines that are equidistant from the three radio beacons will intersect at a point, which is the location of the airplane.

Cryptography

Perpendicular bisectors are also used in cryptography to create secure communication channels. This is done by using the circumcenter of a triangle to encrypt a message, which can only be decrypted by someone who knows the location of the circumcenter.

Conclusion

Perpendicular bisectors are an important concept in geometry that have various applications in different fields. They are used to construct triangles, determine the location of objects in navigation systems, and create secure communication channels in cryptography. Understanding the concept of perpendicular bisectors is essential for anyone studying geometry or working in fields that use geometry.

The Parallel Lines Property Theorem: Understanding its Definition and Applications

The parallel lines property theorem is a fundamental concept in geometry that deals with the properties of parallel lines and their relationship with other lines and angles. In this article, we will provide a definition of the parallel lines property theorem and explore its applications in various contexts.

Definition of the Parallel Lines Property Theorem

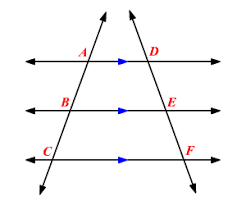
The parallel lines property theorem states that if two parallel lines are intersected by a third line, also known as a transversal, then the corresponding angles are congruent, the alternate interior angles are congruent, and the consecutive interior angles are supplementary.

Corresponding angles are angles that are in the same relative position on different parallel lines with respect to the transversal. Alternate interior angles are angles that are on opposite sides of the transversal and inside the parallel lines. Consecutive interior angles are angles that are on the same side of the transversal and inside the parallel lines.

Applications of the Parallel Lines Property Theorem

The parallel lines property theorem has various applications in geometry and other fields, some of which are highlighted below:

Construction of Triangles

The parallel lines property theorem is used to construct triangles. To do this, we draw two parallel lines and a transversal that intersects them. We can then use the corresponding angles to determine the measurements of the angles in the triangle, allowing us to construct it accurately.

Engineering and Architecture

The parallel lines property theorem is used in engineering and architecture to design and construct buildings, bridges, and other structures. It is important to ensure that the angles in the structures are accurate to prevent collapse or other structural problems.

Navigation Systems

The parallel lines property theorem is used in navigation systems to determine the direction of travel. For example, if a ship is traveling in a straight line and passes two lighthouses that are visible on the horizon, it can use the parallel lines property theorem to determine its heading and direction of travel.

Conclusion

The parallel lines property theorem is a critical concept in geometry that has various applications in different fields. It is used to construct triangles accurately, design and construct buildings and bridges, and navigate through different environments. Understanding the parallel

Understanding Angles: Exploring Right Angles, Acute Angles, and Obtuse Angles

Angles are a fundamental concept in geometry that help us understand the relationship between lines and shapes. In this article, we will explore three types of angles: right angles, acute angles, and obtuse angles.

Right Angles

A right angle is an angle that measures exactly 90 degrees. It is formed when two lines intersect each other perpendicularly, meaning they form a 90-degree angle where they meet.

One real-world example of a right angle is the corner of a square or rectangle. In these shapes, all four corners are right angles, and they help make the shape strong and stable.

Acute Angles

An acute angle is an angle that measures less than 90 degrees. It is formed when two lines intersect each other at an angle that is less than 90 degrees.

One example of an acute angle in the real world is the angle of a sharp pencil. The point of the pencil is formed by two lines that come together at a very acute angle, making it sharp and precise for writing.

Obtuse Angles

An obtuse angle is an angle that measures more than 90 degrees. It is formed when two lines intersect each other at an angle that is greater than 90 degrees but less than 180 degrees.

One real-world example of an obtuse angle is the angle formed by the hands of a clock when it is between 9 and 3 o'clock. The angle between the hands is greater than 90 degrees but less than 180 degrees.

Conclusion

Understanding angles is an essential part of geometry and helps us understand the relationships between shapes and lines. By exploring right angles, acute angles, and obtuse angles, we can better understand the world around us and how it is constructed.

Understand the Problem

The first step in solving any word problem is to understand what the problem is asking. Read the problem carefully and identify the key information, such as the numbers and operations involved. Try to visualize the problem in your head or draw a diagram to help you understand it better.

Choose the Right Operation

Once you have a clear understanding of the problem, decide whether you need to use addition or subtraction. Look for keywords in the problem that indicate which operation to use. For example, if the problem says "more than" or "increased by," you should use addition. If it says "less than" or "decreased by," you should use subtraction.

Organize the Information

Organizing the information in a problem can help you solve it more easily. Write down the numbers and operations involved and label them clearly. You can use a table or a diagram to organize the information. This will also help you avoid making mistakes and ensure that you have considered all the information provided.

Check Your Answer

Once you have solved the problem, always check your answer to make sure it makes sense. Re-read the problem and make sure your answer matches the question asked. Check your calculations to ensure you have not made any mistakes.

Practice, Practice, Practice

The more you practice solving mixed addition and subtraction word problems, the better you will become. Look for online resources or textbooks that provide practice problems and work through them. Practice solving problems in different contexts, such as in real-life situations or in story problems. This will help you develop a deeper understanding of the concepts involved.

Conclusion

Mixed addition and subtraction word problems can be challenging, but with practice and the right strategies, you can become proficient in solving them. Remember to understand the problem, choose the right operation, organize the information, check your answer, and practice regularly. These tips will help you become a confident problem solver in math.